Prologue
This is a record of a workshop on statistics held among the High-Energy Physics group of National Taiwan University in 2022.
The textbook referred to throughout the record is Behnke, O. (2013) Data analysis in high energy physics a practical guide to statistical methods / edited by Olaf Behnke…[et al.]. 1st ed. Weinheim, Germany: Wiley-VCH.
In this week, we covered Sec.2.4–2.6, which was mainly about the method of least squares and maximum-likelihood fits.
The workshop was to let the participants reproduce the histogram fitting on \(M_{\mu^+\mu^-}\) in Subsubsec.2.4.2.1.
Tools1
np.concatenate
a = np.asarray([1, 2])
b = np.asarray([3, 4])
c = np.concatenate((a, b)) # Note the ntuple!
print(c)[1 2 3 4]plt.hist
Does not just draw a histogram, but also returns the histogram and the bins in use.
Least-Squares Fit
Prepare pseudo-data and histograms
By inspection and information given in the book, it seems that
- the number of bins is 60,
- the background events can be simulated by
st.uniform(loc=2, scale=2)and the event number is roughly 1000, and - the signal events can be simulated by
st.norm(loc=3.1, scale=0.05)and the event number is roughly 100.
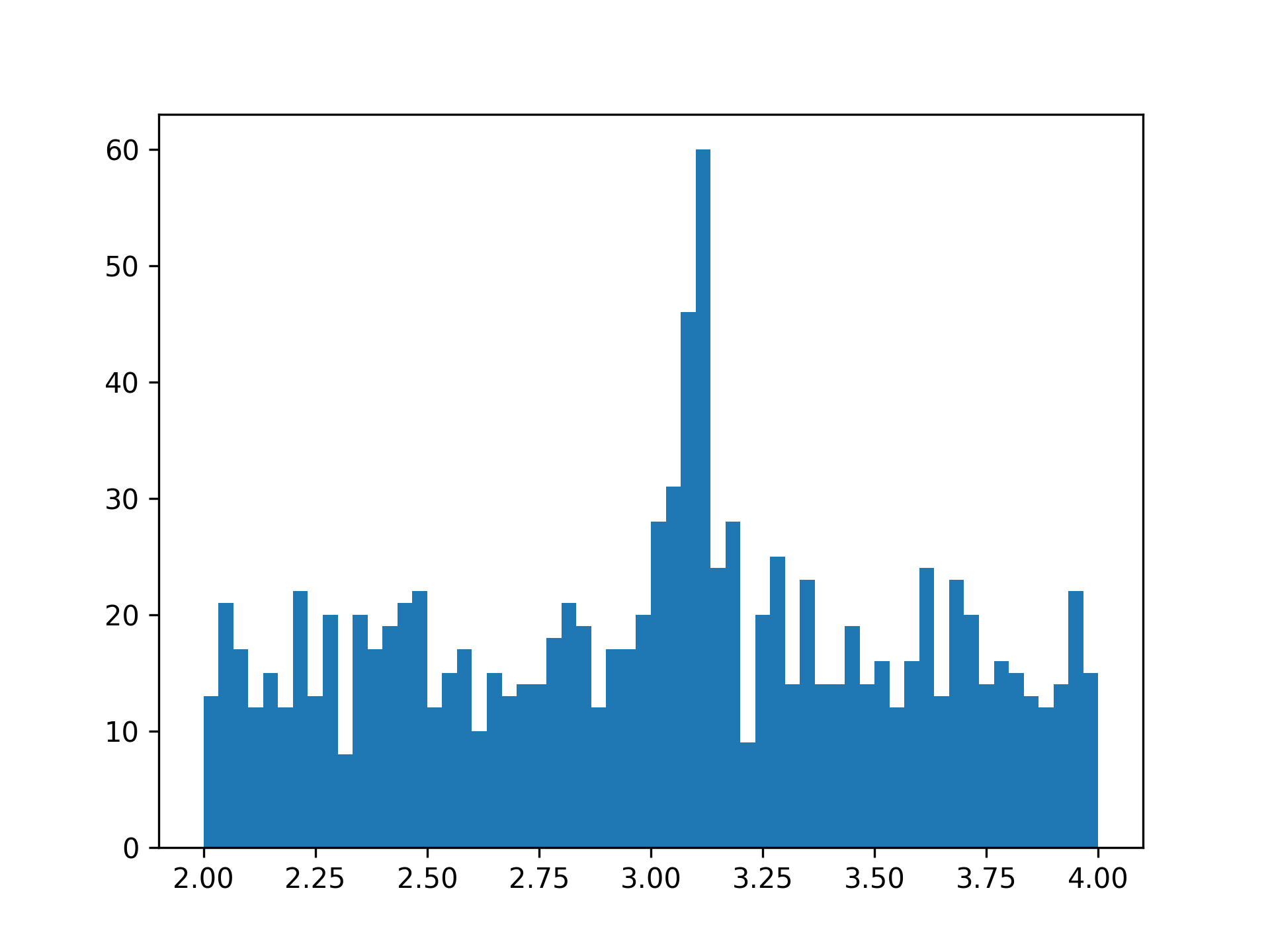
Construct expected number of events in each bin
Assuming we know the exact numbers of background and signal events, then the number of events in each bin is just \[f_i = 1000 \cdot f^B_i + 100 \cdot f^S_i,\] where \(f^B_i\) and \(f^S_i\) are probabilities of events in the \(i\)-th bin i.e.
\[\begin{aligned} f^B_i &= \int^{x^{\mathrm{up}}_i}_{x^{\mathrm{low}}_i} f^B(x) \,dx, \\ f^S_i &= \int^{x^{\mathrm{up}}_i}_{x^{\mathrm{low}}_i} f^S(x;M) \,dx. \end{aligned}\]
In the discrete case, we can approximate the integral as \[f^B_i = \int^{x^{\mathrm{up}}_i}_{x^{\mathrm{low}}_i} f^B \,dx \approx \sum_i f^B(x^c_i) \,\Delta x_i,\] and so on, where \(x^c_i\) is the center of the bin i.e. \(x^c_i = (x^{\mathrm{up}}_i+x^{\mathrm{low}}_i)/2.\)
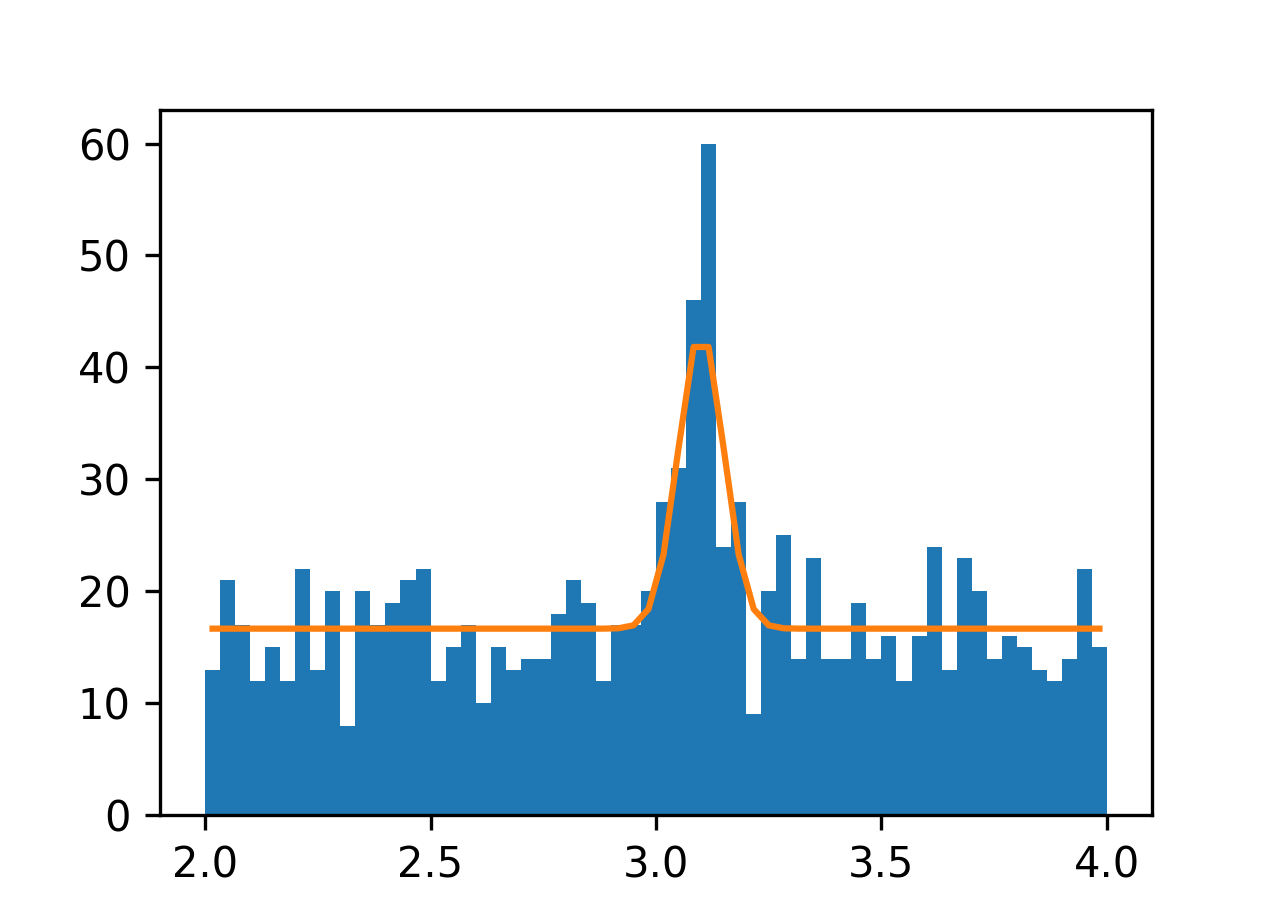
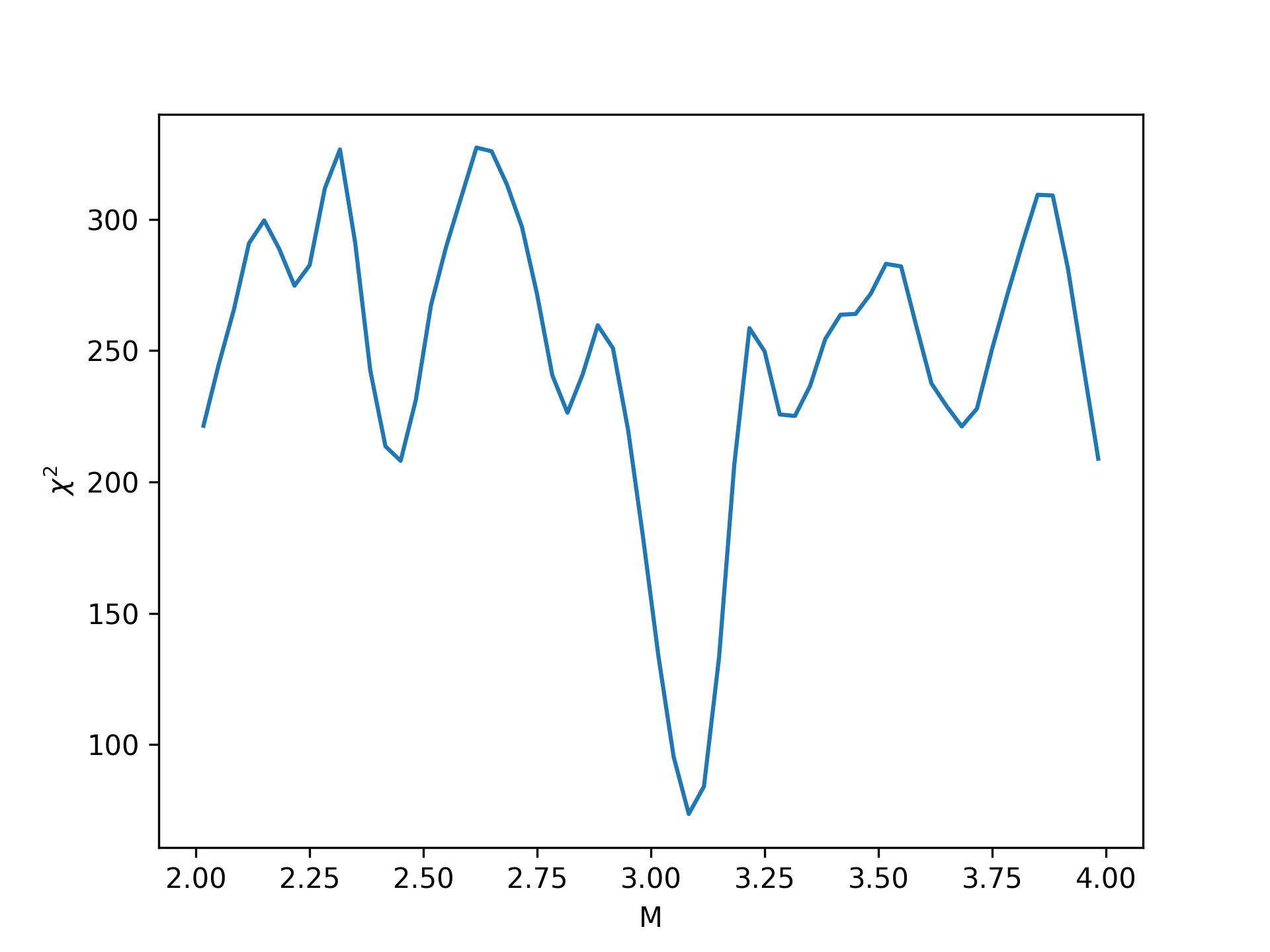
Calculate, plot and minimize \(\chi^2\)
Recall that the (Neyman’s) \(\chi^2\) value can be calculated as \[\chi^2(M) = \sum_{\text{bin} i} \frac{\Big[k_i - f_i(M)\Big]^2}{k_i}.\]
Binned Maximum-Likelihood Fits
Use the same dataset (and the same histogram) to perform Binned MLE. Note that the log-likelihood in the binned case is \[\ln L(M) = \sum^B_{i=1} k_i \ln P_i(M) + \textrm{constant},\] where \(P_i(M)\) is the likelihood computed with the probability of events falling within the \(i\)-th bin.
Remarks
On Numbers of Generated Events
What would happen if we only generated st.norm.rvs(loc=3.1, scale=0.05, size=100) and set bins as np.linspace(-5, 5, 101) instead? What assumption of Least-Squares Fit would be violated? What Python error would you get?
On Assumptions of Event Numbers
Recall that we assume that we know the exact numbers of both signal and background events. That is not a common situation in practice, though. We typically need to turn those event numbers into parameters as well. And that is what the next week’s workshop is about, Extended Maximum-Likelihood Fits.
On \(\chi^2_\textrm{min}\)
You may get \(\chi^2_\textrm{min}\) deviated from the expected value, which is 59, as much as, say, 68. Do you think it’s reasonable? (Hint: go the wikipedia page of \(\chi^2\) distribution and look for the quantity related to expected deviation from the expected value.)
It’s assumed that you’ve already imported the familiar modules i.e.
import numpy as np; import matplotlib.pyplot as plt; import scipy.stats as st; import scipy.optimize as opt.↩